Mouvement et interaction - Spécialité
Mouvement dans un champ uniforme
Exercice 1 : Déterminer une hauteur grâce à l'energie mécanique
Un pistolet en mousse tire des projectiles avec une vitesse de \(15 m\mathord{\cdot}s^{-1}\).
Les balles en mousse sont des sphères de diamètre \(10 cm\) et de masse \(76 g\).
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
Exercice 2 : Variation d'énergie potentielle
Un marcheur de montagne de \( 60 kg \) démarre à une altitude de \( 2290 m \), et finit sa marche au bout de \( 5 h35 \) à \( 1850 m \) d'altitude.
Il a parcouru pendant sa journée \( 17 km \).
On considère que l'intensité de pesanteur vaut \( g = 9,81 m\mathord{\cdot}s^{-2} \).
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
Exercice 3 : Problème sur l'énergie mécanique (jet de projectile)
Les balles en mousse sont des sphères de diamètre \(5\:cm\) et de masse \(62\:g\).
Données
- - Intensité du champ de pesanteur : \( g = 9,80665\:m\mathord{\cdot}s^{-2} \)
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
En supposant que l'énergie cinétique transmise aux balles est la même que dans l'expérience précédente, déterminer la nouvelle hauteur maximale à laquelle on peut envoyer les balles.
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
Déterminer la masse des nouveaux projectiles.
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
Exercice 4 : Rappel de formules sur l'énergie et la vitesse
Un sportif intrépide tente de battre le record de saut en longueur à moto.
L’axe \( Ox \) est le niveau de référence des énergies potentielles de pesanteur.
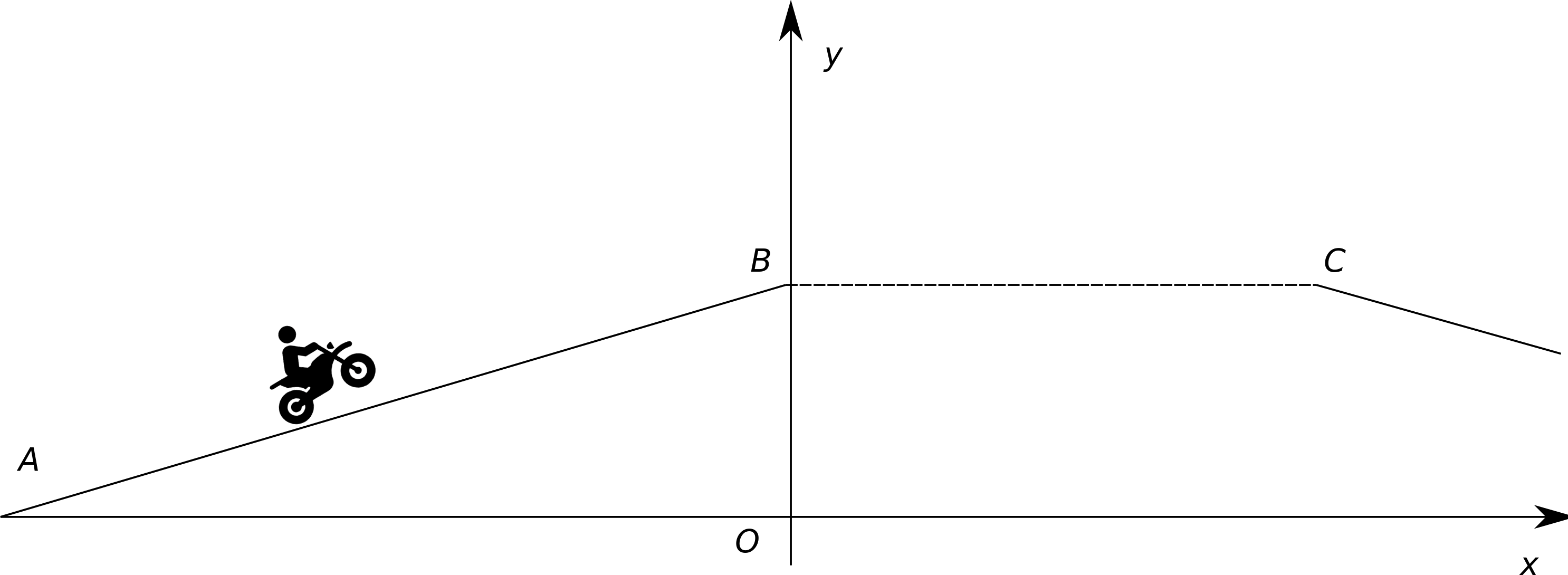
- Intensité de la pesanteur : \( g = 10 m\mathord{\cdot}s^{-2} \)
- Masse du système : \( m = 170 kg \)
- \( AB = 41 m \)
Soit un tremplin incliné d’un angle \( \alpha = 27° \) par rapport à l'axe \( Ox \).
On considère que le motard parcourt le tremplin \( AB \) avec une vitesse de valeur constante égale à \( 164 km/h \).
Au point \( B \) il s'envole pour un saut d’une portée \( BC = 130 m \).
Entre \( B \) et \( C \), toute force autre que le poids est supposée négligeable.
On donnera un résultat avec 3 chiffres significatifs, en \( km / h \) et suivi de l'unité qui convient.
Exercice 5 : Énergie cinétique et force de freinage
Une skieuse, de masse \( m = 62 kg \) avec son équipement, s'élance depuis le haut d'une piste avec une vitesse initiale \( v_{0} = 3 m\mathord{\cdot}s^{-1} \).
Le dénivelé total de la piste est de \( 150 m \).
On considère que l'intensité de pesanteur est la même du haut au bas de la piste, et vaut \( g = 9,8 m\mathord{\cdot}s^{-2} \).
On donnera la réponse avec 2 chiffres significatifs et suivie de l'unité qui convient.
On donnera la réponse avec 2 chiffres significatifs et suivie de l'unité qui convient.
En bas de la piste, la skieuse possède une vitesse \( v_{1} = 84 km\mathord{\cdot}h^{-1} \).
Calculer l'énergie cinétique \( E_{c1} \) de la skieuse en bas de la piste.On donnera la réponse avec 2 chiffres significatifs et suivie de l'unité qui convient.
On donnera la réponse avec 2 chiffres significatifs et suivie de l'unité qui convient.
On donnera la réponse avec 2 chiffres significatifs et suivie de l'unité qui convient.
On donnera la réponse en \(km.h^{-1}\), avec 2 chiffres significatifs.